Answer-first summary for fast verification
Answer: USD 34.03 million of 5-year swaps, and USD 47.74 million of 10-year swaps
C is correct. To determine the notional amounts of the 5-year and 10-year swaps required to hedge USD 100 million notional amount of 7-year swaps, it must be understood that the P&L of the position is given by: -F⁷(DV01⁷/100)Δy⁷ - F⁵(DV01⁵/100)Δy⁵ - F¹⁰(DV01¹⁰/100)Δy¹⁰ in perfect hedge the P&L would equal zero. Substituting the predicted change in the 7-year swap rate from the regression equation into the P&L equation given above, and retaining only the terms related to the changes in the 5-year and 10-year swap rates gives the following equation for the P&L: [F⁷(DV01⁷/100)β⁵ - F⁵(DV01⁵/100)]Δy⁵ + [F⁷(DV01⁷/100)β¹⁰ - F¹⁰(DV01¹⁰/100)]Δy¹⁰
Author: LeetQuiz Editorial Team
Ultimate access to all questions.
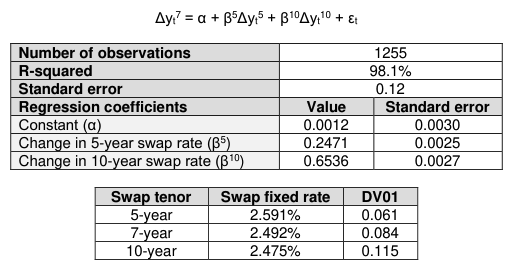
A derivatives trader at an investment bank is considering how to hedge a relatively illiquid 7-year USD interest-rate swap the bank just entered into as the fixed-rate payer. The trader recognizes that any profit resulting from the bid-ask spread may be lost if the trader is hedged with another illiquid 7-year swap and considers using the more liquid 5-year and 10-year USD interest-rate swaps as a hedge. To evaluate this possible hedge, the trader runs a two-variable regression model using changes in the 5-year and 10-year swap rates to explain changes in the 7-year swap rate. The regression model, regression results, and information about the swaps are given below:
What are the correct notional amounts of 5-year and 10-year swaps needed to hedge a USD 100 million notional amount of 7-year swaps?
A
USD 23.76 million of 5-year swaps, and USD 65.81 million of 10-year swaps
B
USD 24.71 million of 5-year swaps, and USD 65.36 million of 10-year swaps
C
USD 34.03 million of 5-year swaps, and USD 47.74 million of 10-year swaps
D
USD 68.85 million of 5-year swaps, and USD 36.52 million of 10-year swaps
No comments yet.